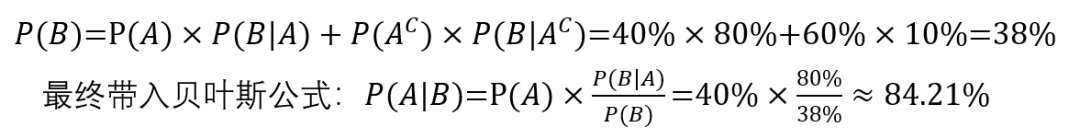提起贝叶斯公式，相信很多同学都会无奈地摇摇头，弯弯绕绕太多了，解题的时候一不小心就会出错。

 

　　今天，我会教大家用侦探的思维方式学习贝叶斯公式，并在此思维方式的基础上为大家总结CFA一级数量方法科目贝叶斯公式考题的标准解题流程，只要大家掌握了套路，并适当练习，以后再也不用担心贝叶斯公式了，哦耶！

 

　　首先，大家把自己想象成一名思维缜密的侦探，现在有一个棘手的案子：

 

　　破案的关键点是确定30年前的某一天是下雨天的概率，这一天就是案发时间，只要当天下雨的概率大于等于75%，就能进一步缩小排查范围，甚至锁定犯罪嫌疑人。

 

　　现在的最困扰的问题是，30年前的信息记录并不像现在这么完善，30年前该地区的每天的天气情况现在找不到直接的线索，走访了气象局等部门后，能得到的信息只是当年降雨的天数占比为40%，也就是说当年任意一天是下雨天的概率是40%，但这个概率只是泛泛而谈，如果没有更加精准的分析，调查就会被迫中止，难道真的要看凶手逍遥法外么？

 

　　就在一筹莫展之际，一位学校小超市的老板娘提供了一丝线索：在下雨天的情况下该超市雨伞当日售罄的概率是80%，在不下雨的情况下该超市雨伞当日售罄的概率是10%，这组概率三十年来一直保持稳定。

 

　　翻开已经泛黄但字迹依然清晰可辨的超市30年前的进货记录登记表，可以发现上面记录着案发当天的雨伞是售罄的。侦探目前拿起纸笔，打算根据这条最新线索，重新评估一下案发当天是下雨天的概率。

 

　　侦探的内心OS:

 

　　在没有这位老板娘提供的最新信息的情况下，当天是下雨天的概率（先验概率）为40%，现在的新信息告诉我，当天雨伞是售罄的，雨伞售罄这件事在下雨天发生的可能性要比在不是下雨天的时候发生的可能性大很多，因此根据新信息调整更新后的当天是下雨天的概率（后验概率）肯定会显著的大于40%，但具体等于多少需要用一下贝叶斯公式。

 

　　哈哈，柳暗花明又一村，看到了破案的希望！

 

　　为了方便标识和套公式，把该地区下雨记为事件A,把该超市的雨伞售罄记为事件B。现在已知的信息为：当年该地区下雨的概率为40%,即P(A)=40%。下雨的情况下该超市雨伞售罄的概率为80%，即P(B|A)=80%。不下雨的情况下该超市雨伞售罄的概率为10%，即P(B|A^C)=10%（A^C读作complement of A，表示A事件的反面，即不下雨）。

 

　　我们现在要求的是P(A|B)，根据贝叶斯公式：P(A|B)=P(A)×P(B|A)/P(B)，贝叶斯公式的本质就是根据新信息对先验概率进行更新调整。到底怎么调整，调整幅度是多少，就看P(B|A)/P(B)这个调整因子有多大了。

 

　　其中P(B|A)是已知条件，而P(B)需要用全概率法则求出，该超市雨伞售罄可以分为两种情况，在下雨天售罄和在不是下雨天的时候售罄，而下雨和不下雨的概率分别为40%和60%，因此：

 

　　

 

　　显然，84.21%大于进一步缩小排查范围需要的最低概率，75%。也是就是说，侦探利用贝叶斯公式在查案上取得了重大突破！

 

 

　　回顾该案件，在运用贝叶斯公式的时候，之所以根据新信息更新后的后验概率比先验概率大很多，是因为调整因子足够大:P(B|A)/P(B)=80%/38%≈2.1

 

　　CFA一级贝叶斯公式解题标准操作流程

 

　　一般需要使用贝叶斯公式的题目问的问题从形式上看肯定是一个条件概率，题中的已知信息会告知一组条件概率，但看着都有点蹩脚，因为已知的这组条件概率跟问题问的角度是岔开的。遇到需要使用贝叶斯公式解题的题目时，按照以下四步走：

 

　　①根据问的问题定义出A事件和B事件。

 

　　由于最终贝叶斯公式计算出的是B事件发生的情况下A事件发生的概率，即P(A|Β)，因此要把题目中的新信息（刚发布的消息/刚刚发生的事情/刚得到的线索等）定义为B事件，在刚才这个案件中，就是该超市雨伞售罄。另外，把题目中已经告知先验概率、现在需要求后验概率的对应的事件定义为A事件，在刚才这个案件中，就是该地区下雨。

 

　　②找出A事件发生的先验概率，并写下来。

 

　　这个概率是后续做调整更新的对象，把这个概率找对非常重要。

 

　　③计算调整因子P(B|A)/P(B)。

 

　　需要注意的是分子P(B|A)一般题目中会直接给出，而分母P(B)一般需要使用全概率法则计算，全概率法则的本质是先分类讨论然后再按照每种情况发生的概率加权平均对应的条件概率。

 

　　④套用贝叶斯公式，P(A|B)=P(A)×P(B|A)/P(B),把第②步和第③步得到的结果相乘就得到了最终的答案。

 

　　以上四步就是CFA一级数量方法科目的考试中，贝叶斯公式问题的标准解题流程。如果大家计算完了之后，想再略微核对一下中间的计算步骤有没有出现明显错误，一个可行的办法是看一下这道贝叶斯公式题目中，新信息B事件是在A事件发生的时候发生的概率更大，还是在A事件不发生的时候发生的概率更大。

 

　　如果是前者（新信息B事件在A事件发生时发生的概率更大），那最终得到的后验概率P(A|B)一定会大于先验概率P(A)。

 

　　如果是后者（新信息B事件在A事件不发生时发生的概率更大），那最终得到的后验概率P(A|B)一定会小于先验概率P(A)。

 

　　如果违反了这样的经验法则，那肯定是在某个步骤中不小心数字代错了。例如在上述案件中，如果最终算出的P(A|B)等于35%，那肯定是算错了，因为先验概率P(A)就有40%，而事件A发生的前提下B事件发生的概率要比A没有发生时B事件发生的概率更大（下雨天该超市雨伞售罄的概率为80%，不下雨的情况下该超市雨伞售罄的概率只有10%），因此P(A|B)不可能小于40%。
 

 

　　相关CFA内容推荐阅读

 

      CFA证书申请条件

 

      CFA考试时间安排